797人阅读已知抛物线的内接的三条边所在的直线均与抛物线相切，求证：三点的纵坐标之和为．
分析与解法一
设三边所在的直线分别为，切点分别为，，且的交点为，的交点为，的交点为，则
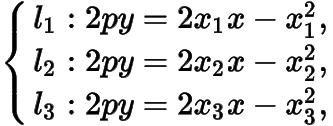
于是有
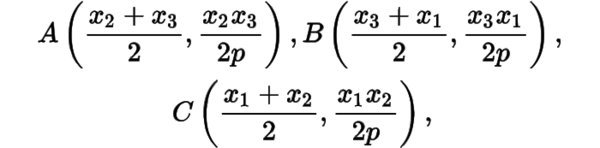
进而由均在抛物线上可得
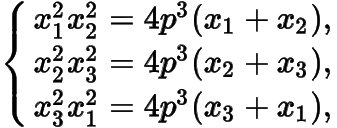
于是可得
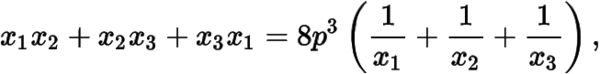
即
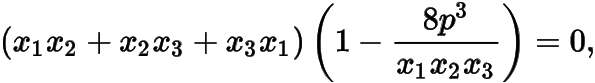
若，则将前面方程组中左右两边分别相乘可得
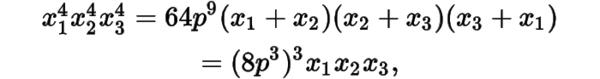
于是有
所以，矛盾；
所以有，进而原命题得证．
法二设，有．从而直线的方程为
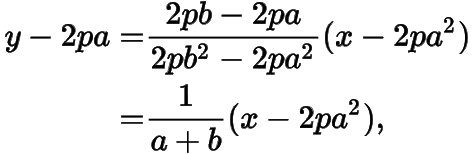
联立的方程与消去得
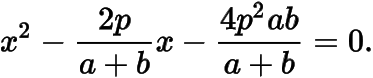
由与相切得判别式
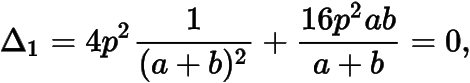
整理得．同理有，两式相减得因为，所以，命题得证．
高校招生
根据学生的高考分数、意向专业，为您查找适合你的院校列表，24小时内短信电话发送给你！直接咨询老师
