
已知椭圆
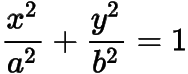
()的离心率
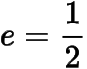
,过焦点且垂直于轴的直线被椭圆截得的线段长为.
(1) 求椭圆的方程;
(2) 斜率为的动直线与椭圆交于两点,在平面上是否存在定点,使得当直线与直线的斜率均存在时,斜率之和是与无关的常数?若存在,求出所有满足条件的定点的坐标;若不存在,请说明理由.
分析与解(1) 根据题意,通径长
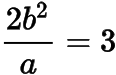
,于是椭圆的方程为
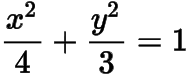
.
(2) 法一 仿射变换
利用仿射变换.设定点的坐标为,平移坐标系,使点为坐标原点,则椭圆方程变为
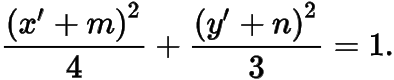
当不过点时,设动直线的方程为,则联立直线与椭圆方程,有
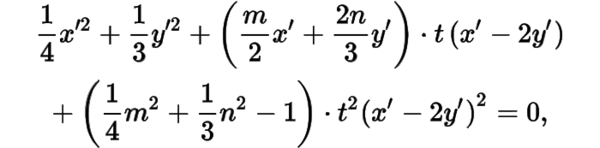
整理得的系数为
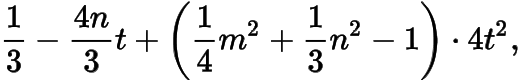
而的系数为
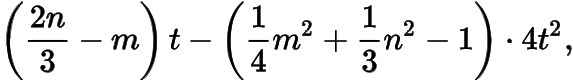
根据题意,直线与直线的斜率之和
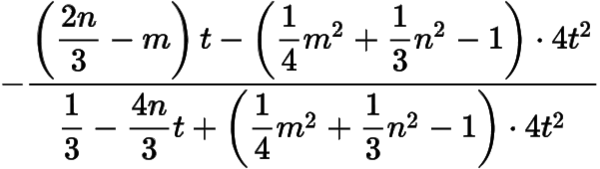
为定值.于是
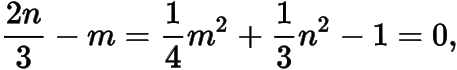
解得,
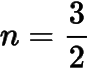
或,
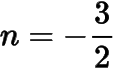
.对应的点在椭圆上,于是不需要考虑过点的情形.
综上所述,所有满足条件的定点的坐标为
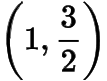
或
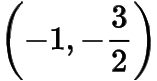
.
注可以将椭圆仿射为圆,则直线的斜率为
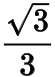
,于是点始终平分弧,进而可取,此时,因此直线与直线的斜率始终互为相反数,符合题意.
法二 直接计算
设
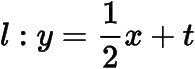
,与椭圆方程联立得设
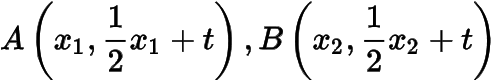
,则有直线的斜率之和
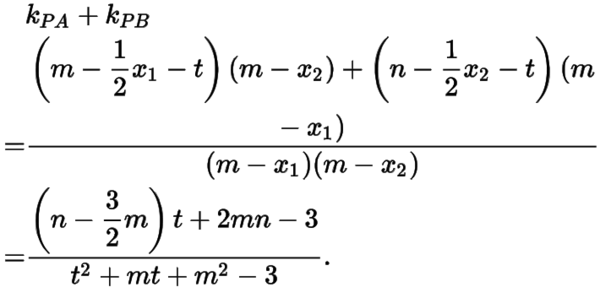
当
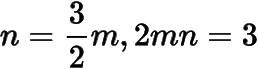
时斜率的和恒为,解得
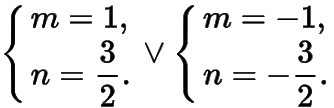
综上所述,所有满足条件的定点的坐标为
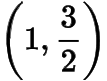
或
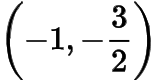
上一篇:对数式的化简与求值
高校招生

根据学生的高考分数、意向专业,为您查找适合你的院校列表,24小时内短信电话发送给你!直接咨询老师