1898人阅读长为 的线段 的两个端点 分别在 轴， 轴上移动，点 在直线 上且满足 ．
(1) 求点 的轨迹方程；
(2) 记点 轨迹为曲线 ，过点 任作直线 交曲线 于 两点，过 作斜率为
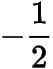
的直线 交曲线 于另一点 ，求证：直线 与直线 的交点为定点（ 为坐标原点），并求出该定点．
分析与解(1) 设，则
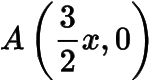
，，于是由可得
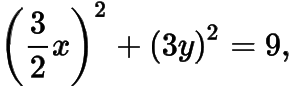
即
．
(2) 利用仿射变换
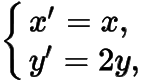
将椭圆
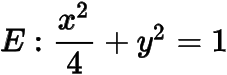
变为圆，，的斜率为，设直线与直线的交点为，把问题转化到圆中加以解决，如图．
连接．由于的斜率为，的斜率为，于是平分弧，进而可得于是四点共圆，四点共圆，有从而与相似，有因此为定值，为定点．转化到原坐标，所求定点为
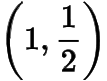
高校招生
根据学生的高考分数、意向专业，为您查找适合你的院校列表，24小时内短信电话发送给你！直接咨询老师
