（2010年广东卷）设，是平面直角坐标系上的两点，现定义由点到点的折线距离．对于平面上给定的不同两点，．

(1) 若是平面上的点，试证明；

(2) 在平面上是否存在点同时满足：和．若存在，请求出所有符合条件的点；若不存在，请说明理由．

分析与解(1) 根据题意，有

因此原命题得证．

(2) 第(1)小题中的不等式取得等号的条件是

即

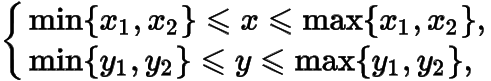
因此当或时，为的中点

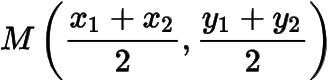
；当且时，点的轨迹是过的中点，斜率的绝对值为，且与直线斜率的符号相反的直线被以线段为对角线各边都与坐标轴方向平行的矩形所截的线段，如图所示．

注对于条件，即因为符号相关，的符号也相反，所以点的轨迹是斜率为或的直线．

若直线的斜率为正，不妨设，则有即点在斜率为的直线上，其它情况可同理．

思考与总结本题中的可以看成是折线段的定义，可以看成是折线垂直平分线的定义．类似的，我们可以定义折线圆，折线椭圆，折线双曲线，点到直线的折线距离

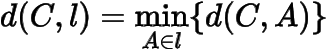
，以及折线抛物线．