1436人阅读(2011年广东卷)设，数列满足，
(，)．
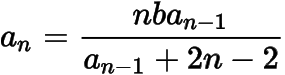
(1) 求数列的通项公式；
(2) 证明：对于一切正整数，
．
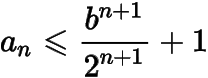
分析与解(1) 当时，
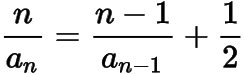
，则数列
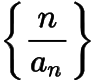
是以
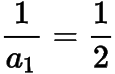
为首项，为公差的等差数列，于是
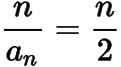
，从而．
当时，
法一有
猜想
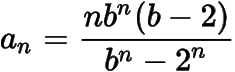
，下面用数学归纳法证明．
当时，猜想显然成立；
假设当时，
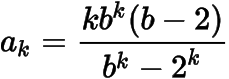
，则
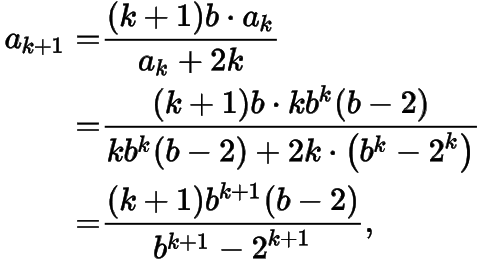
所以当时猜想亦成立．
综上，猜想得证，因此
，．
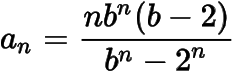
法二由
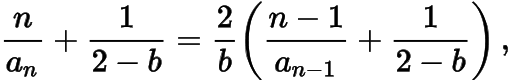
可得数列
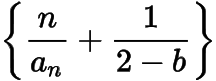
是以
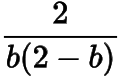
为首项，为公比的等比数列，于是
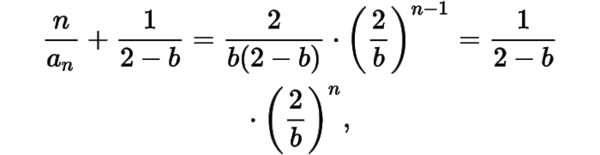
于是
．
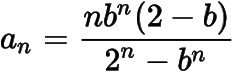
(2) 当时，，
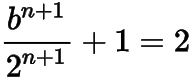
，于是
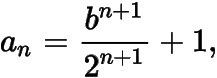
从而原不等式成立；
当时，
法一欲证明不等式即
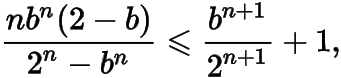
整理知也即证
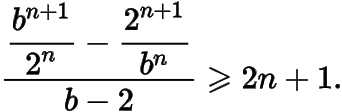
设不等式左侧为，注意到
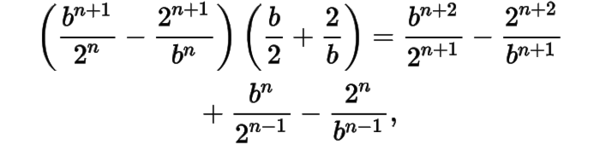
于是
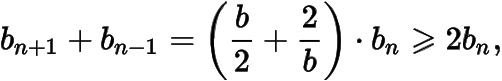
所以考虑到
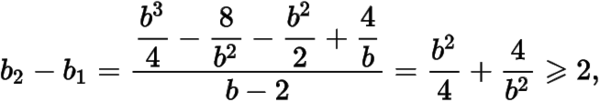
而
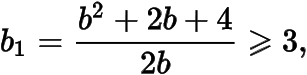
于是．
法二用分析法，有
由均值不等式，上述不等式成立，因此原命题得证．
下一篇：92个本科类专业质量标准即将颁布
高校招生
根据学生的高考分数、意向专业，为您查找适合你的院校列表，24小时内短信电话发送给你！直接咨询老师
