2821人阅读已知，若，且对任意恒成立，则的最大值为________．
分析与解．
法一 去对数
题意即
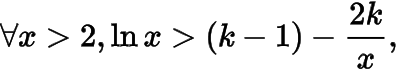
即
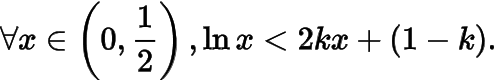
取在
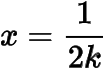
处的切线，有
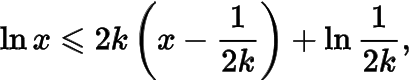
于是只需要
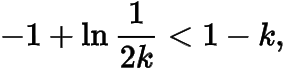
即容易验证的最大值为．
法二 分离变量
题意即
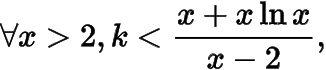
设右边为，则
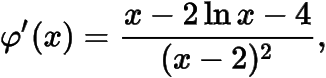
由于
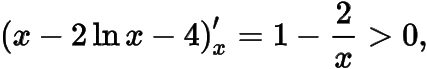
于是有唯一零点，从而的极小值，亦为最小值
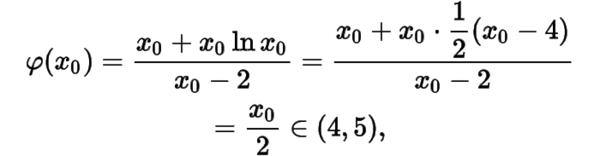
于是的最大值为．
法三 不分离变量
题意即记左边为函数，则是增函数，因为是考虑的最大值，所以考虑有零点的情况，此时当时，取到最小值
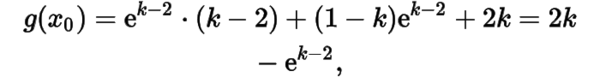
所以即，所以为最大值．
下一篇：指对幂比大小
高校招生
根据学生的高考分数、意向专业，为您查找适合你的院校列表，24小时内短信电话发送给你！直接咨询老师
